Bem vindo à revisão de álgebra linear. Aqui irei mostrar o básico de álgebra linear, tentando . Esse tutorial foi feito visando os fundamentos para os tutoriais de WebGL, mas podem ser usados em qualquer outra aplicação.

Fundamentos

Nestes fundamentos, mostraremos o básico de vetores, matrizes, sistemas de coordenadas. Tentarei colocar o máximo de ilustrações para obter uma visão geométrica de cada informação matemática. Além disso, tentarei passar o conteúdo numa visão top-down, passando primeiro pelos problemas do dia-a-dia, para depois formalizar estes problemas em conceitos matemáticos.

Um bom livro disponível na Internet na íntegra é o livro de Jacir J. Venturi de Álgebra Vetorial e Geometria Analítica. Certas partes se tornam narrativas históricas, tornando a leitura prazerosa. Ele cobre diversos aspectos e propriedades dos vetores que nós usaremos nesses tutoriais, nas disciplinas da área de Processamento Gráfico e no dia-a-dia no desenvolvimento de projetos de visualização gráfica.

Geralmente os vetores são utilizados para representar deslocamentos ao invés de posições imediatas. Em alguns momentos precisamos trabalhar com deslocamentos:

• De uma cidade para outra, traça uma seta representando seu deslocamento;
• Em um segundo, o carro se desloca de um ponto a outro. Se olharmos de cima, podemos traçar uma seta da origem para o destino;
• Os fótons dos raios solares batem na superfície do espelho e refletem como se fossem bolas quiquando. O sentido e direção desses fótons são importantes para sabermos se eles vão atingir o seu olho (se percebes o raio refletido) ou não;
• Se aplicares um soco num saco de boxe (soco num saco, parece uma cacofonia...), a parte inferior do saco vai para o sentido do murro aplicado, com uma aceleração e velocidade iniciais. A ponta no alto está presa no teto, e como a altura do saco é finita e por causa da força centrípeta, o saco tende a subir. Mas aí o sentido da velocidade se orienta para cima, contra a gravidade. A gravidade reduz a velocidade, fazendo com que o saco pare e depois ganhe velocidade no outro sentido. Devido à pressão do ar, a energia não é conservada, tornando o sistema estável. Tudo isso para dizer que velocidade, gravidade, força do soco e do vento podem ser modeladas como vetores;
• Em circuitos elétricos, existem componentes para controlar a passagem de elétrons como resistores e indutores. A resistência e reatância compõem a impedância, e é onde os campos elétricos e magnéticos são estudadas em conjunto, como campos eletromagnéticos. Porém esses campos contém polarizações diferentes (90 graus de diferença de fase). A polarização pode ser modelada como vetores;

Existem milhares de exemplos e aplicações que utilizam vetores e outros conceitos de álgebra linear. Como criar um conceito matemático que seja básico o suficiente para atender tamanha variedade de aplicações? Vamos entender o que é o vetor. Mas antes disso vamos entender o sistema de coordenadas cartesiano.

Sistemas de Coordenadas Cartesiano

Eu vou usar uma didática do livro 3D Math Primer for Graphics and Game Development que é bastante intuitivo.

Uma dimensão

Números naturais, também chamado de números contáveis, foram inventados há bastante tempo, provavelmente para contar ovelhas (um bom livro que estou tentando ler sobre a história da matemática é o livro de Howard Eves, Introdução à História da Matemática). O conceito de uma ovelha fica bastante claro. Duas e três também. Mas depois disso se torna tanta ovelha que era apenas referenciado como "muitas ovelhas". Quando crianças, nós temos um pensamento logarítmico (a diferença entre 1 e 2 é muito maior do que 101 e 102) (vide isto e isto). Inclusive muitos adultos ainda se abstém desse pensamento, quando as habilidades de percepção de escala linear dos números não são desenvolvidos com a escola formal. Com o tempo, civilizações evoluíram a tal ponto de terem pessoas dedicadas a estudarem os números, ao invés de apenas matar e comer ovelhas. Com isso, o conceito de zero (sem ovelha) foi introduzido no sistema numérico, além de criarem vários sistemas gráficos que pudessem representar mais precisamente a quantidade muitos.

O hábito de criar uma fila de ovelhas para contar teve como consequência a linha numérica, ou seja, uma linha com números posicionados em intervalos regulares.

Em algum momento, houve a necessidade de definir o conceito de débito, ou seja, de ficar devendo ovelhas. Daí surgiram os números negativos.

E os pobres que não podem ter uma ovelha inteira, apenas uma parte dela? Com o tempo, foi-se necessário inserir o conceito de números racionais, facilmente posicionados na linha numérica. Para não ficar escrevendo tanto número como 31415/10000, inventou-se o número decimal, como 3,1415.

Depois perceberam que alguns números importantes não podiam ser representados por números racionais, como a razão entre o perímetro da circunferência e seu diâmetro. Estes são os números irracionais, que requerem um infinito número de casas decimais. Enquanto que os números racionais podem ser contáveis, fazendo um mapeamento bijetor para números naturais, os números irracionais não são contáveis. Com isso, duas das maiores áreas da matemática nasceram: a matemática discreta e a matemática contínua.

Pode ser que penses: não dá para representar fielmente o mundo por parecer contínuo devido a quantidade absurda de átomos, quarks e outras partículas. Mas aí é onde entre a Primeira Lei da Computação Gráfica

Se parecer Ok, então está Ok.

Duas dimensões

E se eu tiver uma quantidade dependendo de outra? E se eu tiver de me localizar? Imaginemos uma cidade hipotética chamada Cartésia. Antes de Cartésia ser formada, só havia um terreno plano vazio. Os arquitetos e engenheiros precisaram um sistema para localizar espacialmente qualquer coisa. Inicialmente se preocuparam com as quadras. Definiram-se direções. Também definiram a origem do sistema (a prefeitura) e cada posição (x,y) equivalia à quantidade de quadras ao norte e ao leste as pessoas teriam de ir.

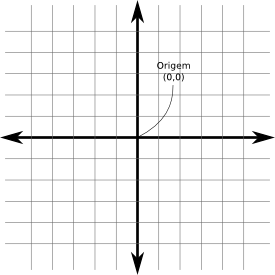
As linhas que passam pela origem se chamam "eixos". Não necessariamente os eixos precisam ser perpendiculares (mas não podem ser paralelas, veremos depois por quê). Há algumas diferenças entre Cartésia e o conceito abstrato de sistema de coordenads 2D:

• Embora a cidade seja limitada, o sistema de coordenadas 2D é ilimitado, se estendendo ao infinito;
• As ruas em Cartésia tem espessura, enquanto que as linhas no sistema abstrato não tem.
• Em Cartésia, só podes dirigir nas rodovias e ruas. Em um sistema de coordenadas, não estás limitado à grade desenhada, apenas ao domínio do números dos eixos.

Podemos denominar o eixo horizontal de eixo \(X\) e o vertical de eixo \(Y\). (5,3), significa 5 quadras no eixo X e 3 quadras no eixo Y.

Mas e (-5, -3)? Precisamos definir uma orientação para qual sentido nos eixos estão os valores positivos. No monitor, a orientação dos números positivos para o eixo X está para a direita, enquanto que para o eixo Y, o sentido está para baixo. Isso se mantém por razões históricas (é o sentido de onde os comandos do DOS, Unix e outros fluem).

Para Cartésia, houve um problema: os profissionais que projetaram Cartésia eram de Disléxia, uma cidade vizinha. Só que eles ficaram confusos sobre qual orientação Cartésia deveria seguir. Toda vez que recebia uma proposta de orientação, o norte aparecia em vários lugares: para cima, para baixo, para a esquerda ou para a direita. Mesmo o prefeito girando o norte para onde ele queria, o sentido do leste estava o contrário do que ele pensava a início. Ele viu que ao todo havia 8 propostas distintas de orientações:

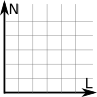
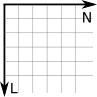
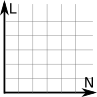
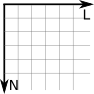
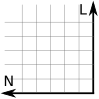
Eles escolheram a primeira como a orientação normal e perceberam que outras três poderiam ser rotacionadas para ficar idênticas à orientação normal. Mas as outras 4 propostas deram trabalho para eles. Apenas no final do dia, quando foram apagar a luz, um dos funcionários percebeu que se colocar uma das outras 4 propostas à contraluz, elas se transformariam à primeira. Ou seja, não importa a orientação no sistema de coordenadas 2D, poderás transformá-la na orientação normal. Depois veremos que em 3D isso não acontece.

3 dimensões

Denominemos o terceiro eixo como eixo-z. Para localizar um ponto no espaço, precisamos de uma terceira coordenada dentro uma tupla \((x,y,z)\).

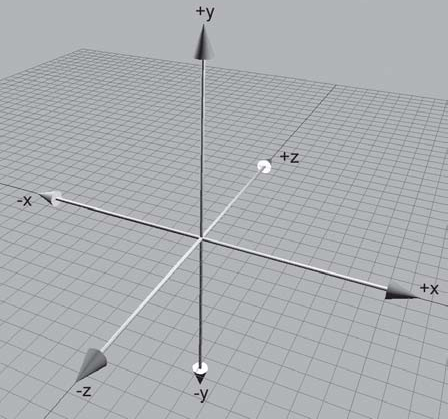
Nem sempre uma orientação pode ser igual a outra, mesmo que rotacione os eixos. Há duas classes de orientações: espaço de coordenadas da mão esquerda e da mão direita. Uma orientação não pode se transformar na outra, embora orientações dentro de uma classe podem se transformar.

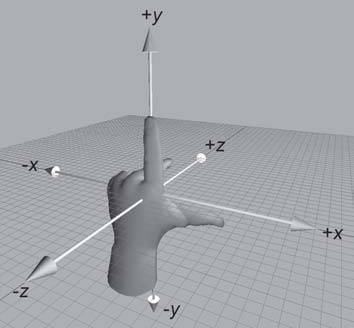
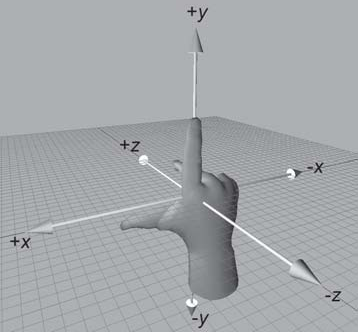
Para a mão esquerda, há uma convenção: coloque o seu polegar no eixo X, os outros dedos no eixo Y (pode ser apenas o polegar), e o eixo Z automagicamente estará saindo da sua palma. Para os sistemas de coordenadas da mão direita, é o mesmo processo. Mas veja que se usares a mão esquerda em um sistema de coordenadas de mão direita, o eixo Z estará saindo das costas da mão. Se seguirmos a ordem X-Y-Z, verás que essa ordem na sua mão direita é polegar-indicador-palma, dando uma orientação antihorária. Essa ordem na mão esquerda resulta numa orientação horária. Então no espaço de coordenadas da mão direita, ângulos positivos seguem a orientação antihorária. Veja como fica a orientação olhando contra o eixo X no sistema de coordenadas da mão esquerda:

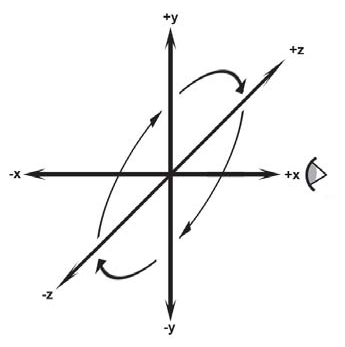
O OpenGL e, por consequência, o WebGL trabalham com o sistema de coordenadas da mão direita. Essa determinação é importante, pois algumas coisas são diferentes entre os dois tipos de sistemas.