Prática 02 CG: Criando polígonos

<< T01: Introdução T03: Adicionando Cores >>

Bem vindo ao meu primeiro tutorial de WebGL! Esta lição é baseado na lição 1 do site LearningWebGL. Nesta lição aprenderemos a exibir um triângulo e um quadrado. É o primeiro passo para criação de ambientes tridimensionais interessantes. Colocaremos em prática as teorias obtidas no curso.

Antes de fuçar o código, o resultado:

Veja o resultado.

Como o ambiente WebGL é mostrado em uma página HTML, vamos inicialmente entender o que é o HTML.

Tarefa: Inicialmente crie uma estrutura de pastas para as lições. Você pode colocar em um servidor local ou remoto. No decorrer dos tutoriais, iremos inserir os arquivos em suas respectivas pastas.

HTML

HTML é uma linguagem de formatação, no qual todas as instruções de formatação estão misturadas com o conteúdo. Os pedaços que compõem um site estão estruturados como uma árvore. As instruções de formatação são chamadas de tags. Todas a página está contida na tag <html>.

Tarefa: Dentro da pasta da lição 1, crie o arquivo index.html. Coloque o seguinte código

<html>
  <head>
    <meta charset="utf-8">
  </head>
  <body>
    Olá mundo.
  </body>
</html>

Essa estrutura minimalista cria uma página apenas com a palavra Olá mundo. O conteúdo deve estar contido entre as tags <body> e </body>. Vínculos para outros arquivos, arquivos de estilo e scripts que tornam a página mais dinâmica geralmente ficam entre as tags <head> e </head>.

Tarefa: Visualize a página no browser. Veja que o código foi interpretado resultando no texto Olá mundo.

Para não haver problemas com acentos, insira a tag meta utilizando o padrão UTF-8.

Na verdade, não queremos exibir Ola mundo. Queremos exibir nosso primeiro ambiente virtual. Na verdade esse ambiente não conterá nada, resultando numa tela vazia e de cor preta (você pode escolher qualquer cor). Todavia, esse exemplo servirá como base para outras lições. As lições serão incrementais.

Veja o resultado: Triangulo Parte 1.

Canvas WebGL

Para poder desenhar, precisamos configurar a tela de desenho. A tela é denominada canvas, e é acessado pela tag <canvas>. O canvas pode exibir tanto conteúdo tridimensional (no contexto do WebGL) como desenhos em bitmap (no contexto do HTML5 2D). Por que duas funcionalidades usando a mesma estrutura? Na verdade o resultado da renderização de um ambiente 3D é uma imagem 2D. Por isso só é necessário um tipo de canvas.

Tarefa: Substitua Olá mundo por

    <canvas id="canvas-webgl" 
	    width="500px" 
	    height="500px" 
	    style="border:none">
    </canvas>

Estamos criando uma tela de tamanho 500x500 e sem borda. Nas primeiras lições, o canvas é a única tag dentro da tag body.

Tarefa: Visualize a página no navegador. Você verá uma página em branco. Se você inspecionar a página (Chrome/Firefox: Botão Direito do Mouse -> Inspecionar Elemento), abrirá o painel de desenvolvedor para depuração da página. Se você selecionar a tag canvas, verá a tela selecionada, evidenciando sua presença.

Vamos agora utilizar o canvas e programar sua inicialização para exibir a demonstração. Utilizaremos a linguagem JavaScript e algumas bibliotecas. Uma delas é a JQuery, o qual facilita a codificação, e o glMatrix, para obter funções para matrizes e vetores.

Tarefa: Adicione o seguinte código dentro da tag head e depois da tag meta

    <meta charset="utf-8">
    <script type="text/javascript" 
	    src="js/gl-matrix-2.4.0.min.js">
    </script>
    <script type="text/javascript" 
	    src="js/jquery-3.2.1.min.js">
    </script>

Todo script deve ser colocado na tag <script>. O código pode estar dentro da própria página ou em um arquivo separado. Como esses dois arquivos serão utilizado por todas as lições, deixamo-los em uma pasta um nível acima dos arquivos das lições.

Obtenha o glMatrix e o jQuery.

Tarefa: Crie outra tag script dessa forma

3 4	`<script type="text/javascript"> </script>`

A página é obtida e interpretada na ordem dada pelo código. Ou seja, todos os scripts são executados na ordem em que estiverem inseridos. Veja que eles estão na tag head, e nesse momento a tag body ainda não foi interpretada. É preciso saber quando toda a página foi processada. O JQuery facilita bastante nesse caso.

Tarefa: Preencha a tag script dessa maneira

    <script type="text/javascript">
      // Iniciar o ambiente quando a página for 
      // carregada
      $(function()
      {
	iniciaWebGL();
      });
    </script>

O $(funcao) é um atalho para $.ready(funcao). O $ faz referência ao documento da página. Isso significa: quando o documento estiver sido processado, execute a função funcao. Ao invés de dizer o nome da função, estamos declarando e implementando a própria função dentro do parâmetro. É uma função anônima.

O que ela faz? Nesse caso estamos chamando a função iniciaWebGL que conterá todo o código para gerar a demonstração.

Tarefa: Crie a função iniciaWebGL

    function iniciaWebGL()
    {
      var canvas = $('#canvas-webgl')[0];
      iniciarGL(canvas); // Definir como um canvas 3D
      iniciarShaders();  // Obter e processar os Shaders
      iniciarBuffers();  // Enviar o triângulo e quadrado na GPU
      iniciarAmbiente(); // Definir background e cor do objeto
      desenharCena();    // Usar os itens anteriores e desenhar
    }

Na linha 3, estamos obtendo a referência do objeto canvas, usando JQuery. Quando você insere o atributo id="identificador" dentro de uma tag, você pode obter a referência "#identificador" para retornar o objeto.

Na linha 4, a função iniciarGL obterá o contexto do WebGL, um objeto que contém toda a funcionalidade para criar e manipular o ambiente 3D, além de enviá-lo para a GPU.

Na linha 5, a função iniciarShaders carrega os shaders. O que são Shaders? Iremos explicar com detalhes.

Na linha 6, a função iniciarBuffers aloca memória na GPU no qual podemos jogar os dados dos objetos 3D (vértices, coordenadas de textura, cores, normais...).

Na linha 7, a função iniciarAmbiente configura o ambiente como um todo.

Na linha 8, a função desenharCena efetivamente manda a GPU gerar a imagem para mostrar no canvas.

Contexto WebGL

O contexto é obtido do canvas. Com ele, você carrega os shaders, desenha os objetos, manda os vértices para a GPU, carrega as texturas e outras coisas mais.

Tarefa: Crie a função iniciarGL

    function iniciarGL(canvas)
    {
      try
      {
	gl = canvas.getContext("webgl") || 
	     canvas.getContext("experimental-webgl");
	gl.viewportWidth = canvas.width;
	gl.viewportHeight = canvas.height;
      }
      catch(e)
      {
	if(!gl)
	  alert("Não pode inicializar WebGL, desculpe");
      }
    }

Aqui estamos tentando obter o contexto WebGL. Se não conseguirmos, então exibe um alerta. Depois de conseguir o contexto, vamos guardar o tamanho do canvas. É que podemos desenhar o ambiente em qualquer tamanho menor ou igual ao tamanho do canvas (por exemplo, desenhando as telas de dois jogadores dentro do canvas em um jogo de corrida). Nesse caso, vamos desenhar o ambiente em todo o canvas.

Shaders

De acordo com o livro Lighting & Rendering, do profissional da Pixar, Jeremy Birn:

Shading é o processo de desenhar, atribuir e ajustar shaders para criar seu aspecto tridimensional. Shaders são definições de como os objetos responderão à luz, descrevendo a aparência de sua superfície e como serão renderizados.

No nosso caso, o shader será uma descrição textual, usando a linguagem GLSL (OpenGL Shading Language) de como um simples conjunto de números (vértices e cores), se converterão em fragmentos (candidatos a pixels), descartando os pixels ocultos e definindo suas cores baseados em cálculos, seja ou não simulando aspectos da luz.

Veja o processo dentro do OpenGL/WebGL

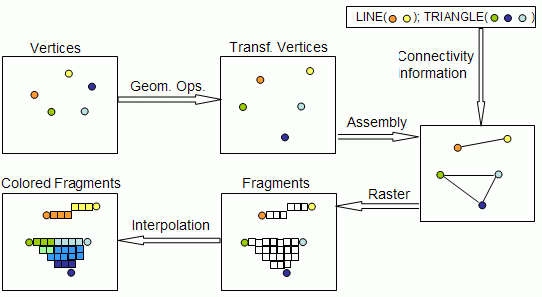
O primeiro passo é criar os vetores de números representando os vértices (posições, cores...).

Além disso, precisamos definir que transformação fazer (rotação, escala, translação, perspectiva, ortográfica...)

Lançamos esses dados para a GPU e ela se encarrega de realizar as operações geométricas no processador de vértices. O resultado disso são os vértices transformados (o segundo bloco).

Após isso, a GPU relaciona os vértices (se são do mesmo objeto ou não). Geralmente são triângulos, todavia podem ser linhas, pontos, entre outros (terceiro bloco).

Para que isso? É que as arestas que conectam os vértices do polígono servirão de base para transformar todo o polígono em pequenos pontos. Esses pontos são os fragmentos (quarto bloco). Essa conversão se dá pelo rasterizador.

Como vai colorir os objetos? Com cada vértice tendo uma cor associada, os pontos intermediários conterão cores intermediárias, interpolando as cores dos vértices nos extremos (quinto bloco).

Todos esses passos são fixos quando é usado o OpenGL de pipeline fixo. Isso significa que você não tem acesso à programação da GPU para mudar algum desses processos.

Com o OpenGL de pipeline programável, você pode criar scripts personalizados para que a GPU transforme os vértices da forma como você quiser (usando o chamado "Vertex Shader") e colorindo os fragmentos como você quiser (usando o chamado "Fragment Shader").

Mas eu transformo e defino cores também no pipeline fixo! Sim, todavia essa transformação e a coloração não são feitas na GPU, e sim na CPU, não aproveitando o paralelismo da GPU.

Uma desvantagem do pipeline programável é que os programas simples se tornam mais complexos. Muito código para fazer um "Alô, Mundo" (que é o caso dessa lição). Mas feito isso, os programas mais complexos se tornam muito mais fáceis.

Iremos criar os dois shaders, compilaremo-los, ativaremo-los e executaremo-los.

Criação do Shader

Vamos criar o script dos shaders de vértice e fragmento.

Tarefa: Adicione os seguintes scripts em qualquer lugar entre as tags <head> e </head>:

    <script id="shader-vs" type="x-shader/x-vertex">
      attribute vec3 aVertexPosition;
      
      uniform mat4 uMMatrix;
      uniform mat4 uVMatrix;
      uniform mat4 uPMatrix;
      
      void main(void)
      {
	gl_Position = uPMatrix * uVMatrix * uMMatrix *
		      vec4(aVertexPosition, 1.0);
      }
    </script>

Vamos explicar o que tem nesse código.

Na linha 1, definimos a tag script com um identificador e um tipo. Nesse caso é um Vertex Shader.

Na linha 2, estamos querendo referenciar a posição do vértice. Esse script executará, em paralelo, para cada vértice.

Nas linha 4, 5 e 6, estamos definindo três matrizes. A primeira é a matriz de modelo. A segunda é de visualização (câmera), e a terceira é de projeção.

Quê? Vamos explicar:

Digamos que os vértices representam o modelo de um carro. Digamos que você queira transladar o seu carro de uma posição para outra. As transformações podem ser representadas por matrizes. Então criaremos uma matriz de translação para ser aplicada ao modelo. Logo, usaremos a matriz de modelo para guardar a transformação.

Além do carro transladado, pode ser que vocẽ no momento esteja o carro pela posição de trás como terceira pessoa (típico de jogo de kart). Então a câmera precisa ser posicionada e orientada de acordo com o desejado. Na verdade não existe um objeto "câmera", o que vamos fazer é posicionar e orientar o mundo todo no sentido contrário (já que as transformações estão sendo aplicadas nos vértices e esses vértices representam o mundo 3D do ambiente, então faz sentido). Por exemplo, se você girar a câmera 30 graus para a esquerda, o mundo vai rotacionar 30 graus para a direita. Essa matriz de posição e orientação do mundo em relação à câmera será guardada na matriz de visualização.

E depois? Bom, quando o carro estiver indo para mais longe (Imagina o piloto Wettel passando de você), então você quer que o carro dele reduza de tamanho por estar mais distante, parecido com o que acontece com o nosso mundo através de nossos olhos. Nesse caso iremos usar a transformação perspectiva. E se na verdade o ambiente 3D for um CAD (Desenho Assistido por computador), onde as dimensões não são influenciadas pela distância? Se estiver desenvolvendo um carro no aplicativo CAD, então dois carros de dimensões iguais não podem ter tamanhos diferentes na tela. Nesse caso, uma projeção ortográfica é usada. Existem outras projeções. O importante é saber que depois de transformar os vértices do modelo e de orientar e posicionar a câmera, precisamos projetar o mundo 3D na tela em 2D, usando a matriz de projeção.

Ok. Mas e o resto do script? Dentro da função main, precisamos dizer qual é a posição final do vértice. Nesse caso usaremos as matrizes MVP (Model-View-Projection) na ordem matemática correta de matrizes (da direita para a esquerda). Então estamos transformando o vértice primeiro usando a matriz de modelo, depois com a matriz de visualização e depois com a matriz de projeção.

E quando a multiplicação pode ser feita da esquerda para a direita? Se você representar os vetores como linhas, ao invés de colunas, e se você usa o sistema de coordenadas baseado na regra da mão esquerda, então a multiplicação deve ser feita da esquerda para a direita.

Mas o que são esses attribute e uniform? Existem propriedades exclusivas de cada vértice (attribute) e propriedades comum a todos os vértices (uniform). Para rotacionar um modelo 3D de um carro, só precisamos de uma matriz para todos os vértices, economizando mémória. Todavia, cada vértice tem sua posição, cor, normal, coordenada de textura, etc...

Após a GPU converter os vértices transformados em fragmentos, o Fragment Shader é executado.

Tarefa: Adicione o seguinte script logo abaixo do script do Vertex Shader

    <script id="shader-fs" type="x-shader/x-fragment">
      precision mediump float;
      
      void main(void)
      {
	gl_FragColor = vec4(1.0, 1.0, 1.0, 1.0);
      }
    </script>

Nesse caso, só precisamos definir a cor do fragmento. E estamos utilizando apenas uma cor fixa (branco). No próximo tutorial aprenderemos como enviar uma cor específica para o shader direto do nosso script.

Mas e os fragmentos escondidos? Se um polígono estiver atrás de outro, então dois fragmentos respectivos serão candidatos a um pixel. Qual deles? Depende do teste de profundidade que você escolher no ambiente. Se você não definir nada, por padrão o último polígono (P1) criado no buffer será desenhado acima do polígono previamente definido no buffer (P2), mesmo que P2 esteja mais perto da câmera do que P1. Dependendo da ordem que você define os vértices das faces de um cubo, a face traseira pode ser desenhada na frente da face frontal, tornando o desenho estranho.

Para corrigir isto, o algoritmo Z-Buffer pode ser usado. Z-Buffer simplesmente descarta o fragmento mais longe da câmera (coordenada Z menor), e usa o fragmento mais perto. Veremos depois como ativar o Z-Buffer.

Nesse script estamos simplesmente definindo a cor dos polígonos como branco. Então a interpolação das cores resultará em todos os fragmentos intermediários como branco. Atente-se que estamos usando vec4 (o quarto componente é o alfa, o nível de transparência). Em lições subsequentes, usaremos esse componente.

Compilação do Shader

Precisamos compilar o shader na GPU. Para isso vamos obter o script, criar um programa, anexar os shaders compilados ao programa e compilar o programa para ele ser usado na GPU. Depois disso obteremos as referências para as variáveis uniforms e atributos para enviar nossos dados de vértices e transformações.

Tarefa: Adicione a função iniciarShaders junto com sua variável para o programa de shader.

    var shaderProgram;
    function iniciarShaders()
    {
      var vertexShader = getShader(gl, "#shader-vs");
      var fragmentShader = getShader(gl, "#shader-fs");
      
      shaderProgram = gl.createProgram();
      gl.attachShader(shaderProgram, vertexShader);
      gl.attachShader(shaderProgram, fragmentShader);
      gl.linkProgram(shaderProgram);
      
      if(!gl.getProgramParameter(shaderProgram, gl.LINK_STATUS))
      {
	alert("Não pode inicializar shaders");
      }
      
      gl.useProgram(shaderProgram);
      
      shaderProgram.vertexPositionAttribute = gl.getAttribLocation(shaderProgram, "aVertexPosition");
      gl.enableVertexAttribArray(shaderProgram.vertexPositionAttribute);
      
      shaderProgram.pMatrixUniform = gl.getUniformLocation(shaderProgram, 
		    "uPMatrix");
      shaderProgram.vMatrixUniform = gl.getUniformLocation(shaderProgram, 
		    "uVMatrix");
      shaderProgram.mMatrixUniform = gl.getUniformLocation(shaderProgram, 
		    "uMMatrix");
      
      
    }
    
    function getShader(gl, id)
    {
      var shaderScript = $(id)[0];
      if(!shaderScript) 
      {
	return null;
      }
      
      var str = "";
      var k = shaderScript.firstChild;
      while(k)
      {
	if(k.nodeType == 3)
	  str += k.textContent;
	k = k.nextSibling;
      }
      
      var shader;
      if(shaderScript.type == "x-shader/x-fragment")
      {
	shader = gl.createShader(gl.FRAGMENT_SHADER);
      }
      else if(shaderScript.type == "x-shader/x-vertex")
      {
	shader = gl.createShader(gl.VERTEX_SHADER);
      }
      else
      {
	return null;
      }
      
      gl.shaderSource(shader, str);
      gl.compileShader(shader);
      
      if(!gl.getShaderParameter(shader, gl.COMPILE_STATUS))
      {
	alert(gl.getShaderInfoLog(shader));
	return null;
      }
      
      return shader;
    }

Muito código, mas vamos explicar o porquê disso. A GPU e CPU são dois componentes distintos do computador e para elas se comunicarem, elas precisam de referências uma da outra. Na CPU, precisamos saber onde colocar a posição do vértice, onde colocar as matrizes. Por parte da CPU, precisamos saber onde está os scripts dos shaders de vértice e fragmento para compilá-los.

Além disso, os shaders compilados não são enviados sozinhos para a GPU, elas estarão associadas a um programa. Um programa pode conter um ou mais shaders de vértices e fragmentos, mas no mínimo deve conter um de cada. Podemos criar vários programas para definir diferentes aparências.

O primeiro objetivo é compilar os shaders. A função getShader realiza essa função. Vamos olhar por partes.

    function getShader(gl, id)
    {
      var shaderScript = $(id)[0];
      if(!shaderScript) 
      {
	return null;
      }

Essa parte captura a tag script que contenha o script do shader. Passamos o identificador e o contexto webgl. Depois disso, precisamos capturar o texto dentro da tag.

      var str = "";
      var k = shaderScript.firstChild;
      while(k)
      {
	if(k.nodeType == 3)
	  str += k.textContent;
	k = k.nextSibling;
      }

Aqui capturamos o objeto representando o texto dentro da script. Dentro do laço, verificamos se ele realmente é um texto (nodeType = 3) e adicionamos seu conteúdo a uma variável de saída. Se houver mais nós de texto dentro da script, o laço continua.

      var shader;
      if(shaderScript.type == "x-shader/x-fragment")
      {
	shader = gl.createShader(gl.FRAGMENT_SHADER);
      }
      else if(shaderScript.type == "x-shader/x-vertex")
      {
	shader = gl.createShader(gl.VERTEX_SHADER);
      }
      else
      {
	return null;
      }

Aqui criamos o objeto do shader dentro do contexto, de acordo com seu tipo (a tag script do shader contém o tipo).

      gl.shaderSource(shader, str);
      gl.compileShader(shader);
      
      if(!gl.getShaderParameter(shader, gl.COMPILE_STATUS))
      {
	alert(gl.getShaderInfoLog(shader));
	return null;
      }
      
      return shader;

Aqui estamos dizendo ao contexto que o código desse objeto shader é o texto do script que capturamos. Em seguida compilamos (ela é enviada para a GPU). Depois perguntamos se a compilação foi um sucesso, alertando-nos em caso de problema. Em seguida retornamos o objeto shader.

Essa função é chamada para cada shader na função iniciarShaders.

Ativação do Shader

A ativação do shader se dá pelo programa, que associa-los-á para sua compilação e uso.

    function iniciarShaders()
    {
      var vertexShader = getShader(gl, "#shader-vs");
      var fragmentShader = getShader(gl, "#shader-fs");
      
      shaderProgram = gl.createProgram();
      gl.attachShader(shaderProgram, vertexShader);
      gl.attachShader(shaderProgram, fragmentShader);
      gl.linkProgram(shaderProgram);
      
      if(!gl.getProgramParameter(shaderProgram, gl.LINK_STATUS))
      {
	alert("Não pode inicializar shaders");
      }

Além de criar os objetos shaders e compilá-los, vamos criar o programa que associará os shaders usando a função attachShader. Em seguida enviaremos o programa para a GPU. Se pararmos por aí, o programa ainda não será utilizado, já que podemos criar vários programas e enviá-lo para a GPU.

      gl.useProgram(shaderProgram);
      
      shaderProgram.vertexPositionAttribute = gl.vertexPositionAttribute = gl.getAttribLocation(shaderProgram, "aVertexPosition");
      gl.enableVertexAttribArray(shaderProgram.vertexPositionAttribute);
      
      shaderProgram.pMatrixUniform = gl.getUniformLocation(shaderProgram, 
		    "uPMatrix");
      shaderProgram.vMatrixUniform = gl.getUniformLocation(shaderProgram, 
		    "uVMatrix");
      shaderProgram.mMatrixUniform = gl.getUniformLocation(shaderProgram, 
		    "uMMatrix");
	
	
    }

Chamando a função `useProgram', agora sim podemos referenciar todos os attributes e uniforms dos shaders. Por isso estamos querendo saber a referência dos atributos, habilitá-los (podemos ter criado vários atributos e habilitar só alguns).

Depois obtemos as referências dos uniforms, que nesse caso são as matrizes MVP. Veja que estamos jogando todas as referências em variáveis do shaderProgram. Você pode colocá-las em qualquer variável. Elas são simples números inteiros.

Buffers

Agora vamos criar os nossos modelos, o triângulo e o quadrado. Nessas primeiras lições, o ambiente será bidimensional, mas poucas linhas o transformam em tridimensional, tanto que colocaremos a coordenada z nos vértices. Por enquanto a coordenada z terá valor 0.

Além dos buffers das posições do vértice, outros dados que precisamos enviar para a GPU são as matrizes de transformação. Elas podem ser qualquer tipo de matriz e serem organizadas de qualquer forma. Vamos utilizar a mais conhecida, que é o modelo Model-View-Projection.

A matriz de modelo (Model) trata de orientar, posicionar e escalar ou cisalhar (distorcer a partir de um eixo) os objetos no mundo. Se você trabalhar com hierarquia de objetos (um esqueleto, por exemplo), você precisa fazer uma composição de transformações de modelo.

A matriz de visualização (View) trata de orientar e posicionar a câmera para ver uma parte do ambiente. Ela é interessante porque quando a câmera se movimenta em um sentido, na verdade o mundo inteiro está se movimentando para outro sentido. Por enquanto colocaremos a câmera no seu padrão (matriz identidade), mas vamos modificá-la nos próximos tutoriais.

A matriz de projeção (Projection) tem o objetivo de colocar todo o mundo tridimensional em um simples plano. Há vários modos para fazer isso. As duas principais são a projeção ortográfica e perspectiva. A projeção ortográfica simplesmente remove uma das coordenadas (nesse caso, removendo a coordenada $z$ para colocar todos os vértices no plano $XY$). A projeção perspectiva trabalha com o modelo de projeção pin-hole, inspirada no modelo visual humano.

A ordem das multiplicações são $P \times V \times M \times \arrow{v}$, da direita para a esquerda, como uma função matemática.

Precisamos criar variáveis para guardar estas matrizes.

Tarefa: Adicione as variáveis globais mMatrix, vMatrix e pMatrix (próximas a tag <script> dentro do código)

var mMatrix = mat4.create();
var vMatrix = mat4.create();
var pMatrix = mat4.create();

var triangleVertexPositionBuffer;
var squareVertexPositionBuffer;

Os buffers guardarão todas as posições do triângulo e do quadrado.

Tarefa: Adicione a função iniciarBuffers:

function iniciarBuffers()
{
  triangleVertexPositionBuffer = gl.createBuffer();
  gl.bindBuffer(gl.ARRAY_BUFFER, triangleVertexPositionBuffer);
  var vertices = [
	0.0, 1.0, 0.0,
      -1.0,-1.0, 0.0,
	1.0,-1.0, 0.0
      ];
  gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);
  triangleVertexPositionBuffer.itemSize = 3;
  triangleVertexPositionBuffer.numItems = 3;
  
  squareVertexPositionBuffer = gl.createBuffer();
  gl.bindBuffer(gl.ARRAY_BUFFER, squareVertexPositionBuffer);
  vertices = [
    1.0, 1.0, 0.0,
    -1.0, 1.0, 0.0,
    1.0,-1.0, 0.0,
    -1.0,-1.0, 0.0
  ];
  gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);
  squareVertexPositionBuffer.itemSize = 3;
  squareVertexPositionBuffer.numItems = 4;
}

Criamos os buffers na GPU para colocarmos os dados dos vértices. O WebGL é uma máquina de estados, e por isso antes de jogar os dados, devemos dizer para qual buffer será enviado. Isso é feito na função bindBuffer.

Para o triângulo, precisamos de 3 vértices (guardado em numItems) de 3 dimensões (guardado em itemSize). Nas outras lições faremos o mesmo padrão de itemSize e numItems para outras propriedades além da posição.

Para enviar os vértices ao buffer, precisamos dizer qual o tipo de buffer, os dados com o tipo desejado e como os dados do buffer vão ser manipulados. STATIC_DRAW significa que não iremos jogar os dados da GPU para a CPU, apenas da CPU para a GPU. Geralmente é o suficiente para nossas lições.

Essa fase apenas lança os dados para a GPU. Se você não modificar os vértices dos modelos, então só precisa enviar apenas uma vez (podes ver que estamos chamando a função iniciarBuffers apenas uma vez).

Ambiente

function iniciarAmbiente()
{
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);
}

Nesse caso, iremos definir a cor do fundo como preto (para destacá-lo na página branca).

Lembra do Z-Buffer? É com gl.enable(gl.DEPTH_TEST) que estamos habilitando o teste Z-Buffer.

Desenhando a Cena

function desenharCena()
{
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
  mat4.perspective(pMatrix, 45, gl.viewportWidth / gl.viewportHeight, 0.1, 100.0);
  mat4.identity(mMatrix);
  mat4.identity(vMatrix);
  
  // Desenhando Triângulo
  var translation = vec3.create();
  vec3.set (translation, -1.5, 1.0, -7.0); 
  mat4.translate(mMatrix, mMatrix, translation);
  gl.bindBuffer(gl.ARRAY_BUFFER, triangleVertexPositionBuffer);
  gl.vertexAttribPointer(shaderProgram.vertexPositionAttribute, triangleVertexPositionBuffer.itemSize, gl.FLOAT, false, 0, 0);
  setMatrixUniforms();
  gl.drawArrays(gl.TRIANGLES, 0, triangleVertexPositionBuffer.numItems);
  
  // Desenhando o Quadrado
  vec3.set (translation, 3.0, 0.0, 0.0); 
  mat4.translate(mMatrix, mMatrix, translation);
  gl.bindBuffer(gl.ARRAY_BUFFER, squareVertexPositionBuffer);
  gl.vertexAttribPointer(shaderProgram.vertexPositionAttribute, squareVertexPositionBuffer.itemSize, gl.FLOAT, false, 0, 0);
  setMatrixUniforms();
  gl.drawArrays(gl.TRIANGLE_STRIP, 0, squareVertexPositionBuffer.numItems);
}

function setMatrixUniforms()
{
  gl.uniformMatrix4fv(shaderProgram.pMatrixUniform, 
		      false, pMatrix);
  gl.uniformMatrix4fv(shaderProgram.vMatrixUniform, 
		      false, vMatrix);
  gl.uniformMatrix4fv(shaderProgram.mMatrixUniform, 
		      false, mMatrix);
}

Precisamos limpar a tela (em uma animação iríamos ver todos os quadros sobrepostos se não limparmos antes de cada desenho), definir a perspectiva (você pode colocar essa linha dentro de iniciarAmbiente caso não queira mudar a perspectiva), preencher as matrizes de modelo e de visualização (não estamos mudando a orientação da câmera, por isso a matriz identidade na matriz de visualização), desenhando o triângulo e desenhando o quadrado.

Limpando a Tela

Você pode limpar a tela usando gl.clear e colocando como parâmetro um número byte que representa que tipo de buffer estará limpo. Nesse caso estamos limpando o mapa de cores (o que você vê no canvas) e o mapa de profundidade (deixar todos os pixels com eixo Z = 0, para não dar problemas no processo de oclusão dos fragmentos escondidos por outros).

Definindo a Perspectiva

Há dois tipos de projeções principais: ortográfica e perspectiva. Existem outros tipos de projeções, como paraperspectiva, ortográfica escalada... Este link contém uma apresentação sobre modelos de câmera e projeções. Livros sobre geometria projetiva como esse de Coxeter trabalha matematicamente essa geometria que trabalha com incidências e que generaliza alguns aspectos sobre outras geometrias (euclidiana, afim...).

Neste exemplo, queremos o efeito de que, quando o objeto estiver distante da câmera, seu tamanho seja reduzido na tela. Como estamos usando a regra da mão direita, com o polegar no eixo $X$, os outros dedos no eixo $Y$ e a palma da mão direcionada para o eixo $Z$, podes ver que o eixo $Z$ está orientado contra a câmera. Se você posicionar a câmera na origem $[0,0]$, então a coordenada $z$ dos objetos visíveis na câmera contém valores negativos.

Mas e se eu quiser valores positivos? Então os objetos estarão "atrás" da câmera. Como vê-los? Orientando a câmera no sentido contrário, usando a matriz de câmera. Nas aulas seguintes trabalharemos melhor estes conceitos.

Então vamos usar a função de projeção perspectiva. Geralmente 45 graus é um campo de visão satisfatório para a maioria das aplicações. Para o ambiente não ficar distorcido, vamos capturar o tamanho do canvas e usar a relação largura/altura. A figura abaixo mostra o frustum (trapezóide) do campo de visão da câmera, um volume de uma pirâmide sem a ápice. Tudo que estiver dentro do volume será visualizado (ou pelo menos transformar-se-á em fragmentos). Veja na figura que o ângulo define a altura, enquanto o aspecto com a altura gera a largura. Esta função trabalha com dimensões no plano near. Os outros parâmetros são a distância dos planos near e far do centro de projeção da câmera. Por último, devemos dizer qual a matriz que guardará essa transformação.

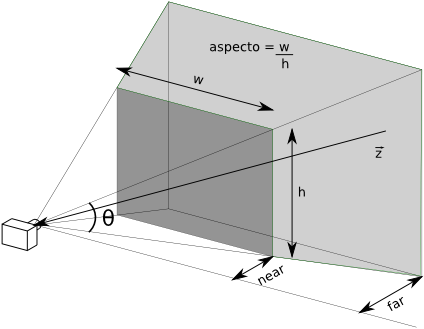
Por enquanto, não vamos deslocar a câmera e nem o modelo. Então insira a matriz identidade nestas variáveis.

Desenhando o triângulo e o quadrado

Veja que os códigos são parecidos para o triângulo e o quadrado. Na verdade deixamos como exercício criar apenas uma função para desenhar tanto o triângulo quanto o quadrado.

Vamos desenhar o triângulo na esquerda e o quadrado na direita. Por isso estamos usamos a translação com (x,y,z) = (-1.5, 0, -7.0). -1.5 no eixo X pois o eixo é crescente na direita, e -7.0 pois o eixo Z é crescente na direção da câmera. Para tornar o objeto mais afastado da câmera, então colocamos valores negativos (na verdade são valores menores do que 0.1).

Depois precisamos dizer ao OpenGL com quais pontos estamos lidando. Isso se faz com gl.bindBuffer(gl.ARRAY_BUFFER, id_do_buffer). Todas as operações de buffer seguintes trabalharão com o buffer indicado (OpenGL é uma máquina de estado). A função gl.vertexAttribPointer associa o buffer que indicamos com o atributo do shader que compilamos. Ou seja, estamos respondendo a pergunta: "Para onde vai os vértices no shader da GPU?". Para esta função, precisamos do endereço do atributo no shader, o tamanho do atributo (se for posição em 3D, então é 3, se o atributo for cor RGBA, então é 4, se for coordenada de textura (s,t), então o valor é 2...), o tipo de dados (pois interamente ele trabalha com bytes), se queremos que os dados estejam na faixa $[-1,1]$ (não queremos isto), o início dos dados no buffer e o local do buffer (queremos desde o começo do buffer e queremos usar o buffer associado na função bindBuffer), por isso estamos colocando 0.

Sabe a função translate que utilizamos antes do bindBuffer. Ela não joga para GPU diretamente a translação. Ela guarda a transformação na variável, pois podemos fazer combinações de transformações antes de enviar para a GPU. Lembre-se que atualmente o OpenGL não trabalha com modo imediato, e sim com o modo retido, para só depois mandar tudo para a GPU. Dessa forma, se você não altera nada no cenário, você não precisa mandar novamente o buffer de vértices nem os uniforms.

Mas quando ele envia estas transformações? Justamente nas funções que colocamos dentro da função setMatrixUniforms. A função gl.uniformMatrix4fv envia uma matriz $4\times 4$ (do tipo ponto flutuante) para o uniform, espaço de memória na GPU que será tratada pelo shader. O uniform é diferente do atributo, pois ela está acessível tanto para o shader de vértice como de fragmento e ela é única para todos os vértices, enquanto que o atributo é específico para cada vértice. O primeiro argumento é o endereço da uniform no shader. O segundo argumento pergunta se queremos a transposta antes de enviar para a GPU. O terceiro parâmetro é efetivamente a matriz.

Após jogar todos os vértices e transformações, devemos desenhá-las. A função gl.drawArrays precisa saber que tipo de forma estamos desenhando, o índice do primeiro vértice no buffer a ser desenhado (já que podemos desenhar partes do buffer, ao invés de desenhar ele todo, nesse caso estamos desenhando todos os vértices de uma vez), e o número de vértices a serem desenhadas.

Conclusão

Ufa! Esse tutorial é muito grande, mas garanto que os outros tutoriais são apenas modificações (poucas linhas de código) em relação ao primeiro. E tem o efeito reverso: enquanto esse tutorial apenas mostra triângulos e quadrados apáticos, outros tutoriais terão efeitos bem mais interessantes com poucas modificações.

Abraços e vejo vocês no segundo tutorial.

T03: Adicionando Cores >>