https://blog.pantuza.com/artigos/busca-binaria
Busca Binária
Quando itens de dados são armazenados em uma coleção, como uma lista, dizemos que eles têm uma relação linear ou sequencial. Cada item de dados é armazenado em uma posição relativa aos outros. Nas listas (vetores) JavaScript, essas posições relativas são os valores de índice dos itens individuais. Como esses valores de índice são ordenados, é possível para nós visitá-los em sequência. Este processo dá origem a nossa primeira técnica de busca, a busca sequencial.
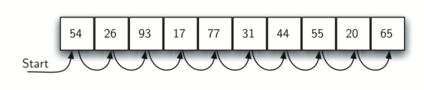
A imagem abaixo mostra como essa pesquisa funciona. A partir do primeiro item da lista, simplesmente passamos de item para item, seguindo o pedido sequencial subjacente até encontrar o que estamos procurando ou ficar sem itens. Se ficarmos sem itens, descobrimos que o item que procuramos não estava presente.
Para a implementação do código em JavaScript. A função precisa da lista e do item que procuramos e retorna um valor booleano para saber se ele está presente. A variável booleana encontrada é inicializada para falso (false) e é atribuído o valor verdadeiro (true) se descobrimos o item na lista.
function buscaSequencial(umVetor, item){
let pos = 0;
let achou = false;
while(pos < umVetor.length && !achou){
if (umVetor[pos] === item){
achou = true;
}
else{
pos = pos+1;
}
}
return achou;
}Análise de Complexidade
No melhor caso, o elemento a ser buscado é encontrado logo na primeira tentativa da busca. No pior caso, o elemento a ser buscado encontra-se na última posição e são feitas N comparações, sendo N o número total de elementos. No caso médio, o elemento é encontrado após (N+1)/2 comparações. O algoritmo de busca linear é um algoritmo O(n).
Busca binaria
Caso você possua uma lista com os valores ordenados de forma numérica ou alfabética, é possível fazer uma busca muito mais rápida. Ao invés de pesquisar a lista em sequência, uma busca binária começará examinando o item do meio. Se esse item for aquele que estamos procurando, a busca termina. Se não for o item correto, podemos usar a natureza ordenada da lista para eliminar a metade dos itens restantes. Se o item que procuramos for maior do que o item do meio, sabemos que toda a metade inferior da lista, bem como o item do meio, podem ser eliminados de uma consideração mais aprofundada. O item, se estiver na lista, deve estar na metade superior.
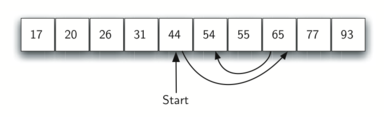
Podemos então repetir o processo com a metade superior. Comece no item do meio e compare-o contra o que estamos procurando. Novamente, encontramos ou dividimos a lista pela metade, eliminando assim uma grande parte do nosso possível espaço de busca. A Figura abaixo mostra como esse algoritmo pode encontrar rapidamente o valor 54.
BUSCA-BINÁRIA (V[], início, fim, e)
i recebe o índice do meio entre início e fim
se (v[i] = e) entao
devolva o índice i # elemento e encontrado
fimse
se (inicio = fim) entao
não encontrou o elemento procurado
senão
se (V[i] vem antes de e) então
faça a BUSCA-BINÁRIA(V, i+1, fim, e)
senão
faça a BUSCA-BINÁRIA(V, inicio, i-1, e)
fimse
fimsedef binsearch(seq, search):
right = len(seq)
left = 0
previous_center = -1
if search < seq[0]:
return -1
while 1:
center = (left + right) / 2
candidate = seq[center]
if search == candidate:
return center
if center == previous_center:
return - 2 - center
elif search < candidate:
right = center
else:
left = center
previous_center = centerpublic static int buscaBinaria(int[] array, int valor){
int inicio = 0;
int fim = array.length-1;
while(inicio <= fim){
int meio = (inicio+fim)/2;
if(array[meio] == valor){
return meio;
}
if(valor > array[meio]){
inicio = meio+1;
} else {
fim = meio-1;
}
}
return -1;
}function buscaBinaria(umVetor, item) {
let prim = 0;
let ult = umVetor.length - 1;
let achou = false;
while (prim <= ult && !achou) {
meioLista = Math.ceil((prim + ult) / 2);
if (umVetor[meioLista] == item) {
achou = true;
}
else {
if (item < umVetor[meioLista]) {
ult = meioLista - 1;
}
else {
prim = meioLista + 1;
}
}
}
return achou;
}Análise de Complexidade A complexidade desse algoritmo é da ordem de Θ(log2 n), em que n é o tamanho do vetor de busca. Apresenta-se mais eficiente que a Busca linear cuja ordem é O(n).
Imagine o seguinte problema: dado um vetor ordenado de n números distintos, faça um programa que responde a m perguntas do tipo: “o número x está no vetor?”. A primeira linha terá dois inteiros: os valores de n e m, respectivamente. A segunda linha terá n inteiros ordenados: os elementos do vetor. A terceira e última linha terá m inteiros. Para cada um desses números, seu programa deve gerar uma linha na saída. Se o número não estiver no vetor, a linha deve ter o valor “-1”. Caso ele esteja, ela deve imprimir a posição do número no vetor (indexado de 1 a n).
Segue um exemplo de entrada e saída:
Entrada: 7 4
-2 0 4 7 8 9 11
5 -2 7 15
Saída:
-1
1
4
-1
Tal problema parece ser bem simples: basta que percorramos o vetor inteiro com um for, procurado o número lido. Porém, percorrer o vetor tem complexidade O(n), e esta operação será executada m vezes, o que gera uma complexidade de **O(n*m)**. E se as únicas restrições do problema forem: \(1\leq n, m \leq 10^5\)? A complexidade será \(O(10^{10})\), o que com certeza iria ultrapassar o tempo máximo de execução. Como fazer para verificar se um número está em um vetor ordenado de maneira mais eficiente?
Esse problema é semelhante a procurarmos uma palavra em um dicionário de n páginas, supondo que basta achar a página. A primeira ideia que tivemos foi folhear, uma a uma, todas as páginas do dicionário, começando da primeira até a última, procurando a palavra. Nos piores casos, teremos que olhar todas as páginas do dicionário. Note que tal mecanismo de busca funcionaria com a mesma eficiência se as palavras do dicionário estivessem em ordem aleatória, ou seja, não estamos usando a nosso favor o fato de as palavras estarem ordenadas. Essa ordenação só nos trás uma vantagem: quando vemos que uma palavra não está em determinada página, sabemos, pela ordem alfabética, se ela, estando no dicionário, estará antes ou depois daquela página, o que elimina todas as outras opções. Assim, vamos tentar eliminar o máximo possível de páginas logo na primeira consulta ao dicionário: basta que o abramos bem no meio! Desse modo, se a palavra estiver lá, que bom que encontramos, se não, não importa se a palavra estará antes ou depois da página do meio, eliminarei metade das consultas que teria que fazer a cada uma das páginas da metade em que a palavra não se encontra. Agora, na metade que restou do dicionário, aplico o mesmo processo, até que só reste uma possibilidade de página em que a palavra pode estar: se ela lá estiver, achei a página, se não, ela não pode estar no dicionário!
E qual a complexidade desse algoritmo? Iremos repetir o processo de dividir o número de páginas possíveis ao meio até que reste somente uma página, logo, sendo c o número de vezes que vou consultar o dicionário temos que: \(\frac{n}{2^c} = 1\Leftrightarrow n = 2^c\Leftrightarrow \log{n} = \log{2^c} = c \log{2} = c\Leftrightarrow c = \log{n}\), logo a complexidade de uma busca é O(log n). Desse modo, realizando \(10^5\) operações de complexidade \(O(\log{10^5})\), teremos uma complexidade final de \(O(10^6)\), o que certamente passa no tempo. Basta gora que implementemos a função que realiza essa busca eficiente no vetor, que é conhecida como busca binária.
Vamos declarar o array de inteiros de nome vetor, que guardará os inteiros ordenados. Agora, vamos declarar a função “int buscab(int x){}”, que irá retornar a posição de x em vetor, ou -1 se ele não estiver no array. A função começará declarando três variáveis: int ini, int fim e int meio, que guardarão o começo, o fim e o meio do intervalo que vamos analisar, respectivamente. O valor inicial de ini será 1 e o de fim será n, pois no começo o número pode estar em qualquer posição do vetor. Ela terá um while que repetirá o algoritmo enquanto o intervalo tiver pelo menos um número (ini<=fim). A ideia é atribuir a meio o elemento mais ou menos na metade do intervalo (meio=(ini+fim)/2;) e verificar se o número do meio (vetor[meio]) é o que procuramos. Se ele for, retornamos o valor de meio. Se procuramos um número menor que o do meio, então agora devemos olhar, na próxima repetição do while, apenas para o intervalo compreendido entre ini e meio-1, pois é onde ele deve estar. Para isso, fazemos fim receber o valor meio-1. Se procuramos um número maior, olhamos, de maneira análoga, para o intervalo compreendido entre meio+1 e fim, com o comando “ini=meio+1;”. Se o while terminar e a função ainda não tiver retornado nada, então o número não está no vetor e retornamos o valor -1. Vale lembrar que os comando aqui usados só são corretos se o vetor estiver indexado de 1 a n, correndo o risco de entrar em loop infinito caso haja a posição 0.
Segue o código que resolve o problema acima com a função buscab, para melhor entendimento:
#include <cstdio>
#define MAXN 100100
int n, m, vetor[MAXN];
int buscab(int x){ // declaro a função buscab, que recebe um int como parâmetro
// declaro os inteiros ini, meio e fim
int ini=1, fim=n, meio; // ini já começa com 1 e fim com n
while(ini<=fim){ // enquanto houver algum elemento no intervalo
meio=(ini+fim)/2; // meio recebe a posição do meio
if(vetor[meio]==x) return meio; // se achei o número, retorno o valor de meio
if(vetor[meio]<x) ini=meio+1; // se o número está na frente, olho para a metade depois de meio
if(vetor[meio]>x) fim=meio-1; // se o número está atrás, olho para a metade antes de meio
}
return -1; // se o while terminar sem a função retornar, o número não está no vetor
}
int main(){
cin >> n >> m; // leio os valores de n e m
for(int i=1; i<=n; i++){
cin >> vetor[i]; // leio os valores do vetor
}
for(int i=1; i<=m; i++){ // para cada pergunta
// leio o número a ser procurado e salvo na int num
int num;
cin >> num;
cout << buscab(num) << "\n"; // e imprimo o valor de buscab(num)
}
return 0;
}A implementação de uma busca binária é conhecida por ter pequenos bugs que quase nunca identificamos, o que a faria entrar em algum loop infinito. Enfim, o código aqui mostrado funciona bem, mas, caso você esqueça algum detalhe, algumas pessoas gostam de colocar um contador dentro do loop que impede que o número de repetições do while passe de 35, por exemplo, visto que o log do maior valor que cabe em um int é 32, evitando o loop infinito.
Vale notar também que a ideia da busca binária não se restringe somente a sequências crescentes, mas a qualquer intervalo em que, buscando determinado elemento, olho para alguma posição do intervalo e sei se ele está antes ou se está depois de tal posição. Certa vez me deparei com um problema em que parte dele consistia em identificar, em \(O(\log{n})\), o maior elemento de um vetor de inteiros positivos que crescia até certo elemento, que era o máximo, e a partir de então começava a decrescer. Segue um exemplo de vetor assim, de 7 elementos:
1 3 4 5 6 4 3
É fácil ver que o elemento é o procurado (o máximo) se o anterior a ele for menor ou igual que ele e o posterior for menor. No caso, 6 é antecedido de 5 e sucedido por 4. Vamos aplicar a busca binária: checar se o número do meio é o maior é checar se seu antecessor é menor que ele e seu sucessor também (“if(vetor[meio-1]<vetor[meio] && vetor[meior+1]<vetor[meio])”). Se isso ocorrer, retornamos o valor salvo em “vetor[meio]”. Note que para a função não dar problema no começo e no fim do vetor, as posições 0 e n+1 devem estar declaradas (n é o número de elementos), e guardarem o inteiro 0, pois ele é menor que todos os elementos do vetor, não quebrando, portanto, sua lógica de ser crescente e depois decrescente, mas nunca serão acessados pela busca binária. Caso o número do meio não seja o maior, olhamos se seu sucessor é menor que ele. Se for, então já estamos na parte do vetor que decresce, e devemos olhar apenas para a metade atrás da posição meio (“if(vetor[meio+1]<vetor[meio]) fim=meio-1;”). Se o sucessor for maior, então ainda estamos na parte que cresce, e devemos olhar a metade depois da posição meio (“if(vetor[meio+1]>vetor[meio]) ini=meio+1;”). Segue a implementação dessa busca binária:
int n, vetor[100100]; // variáveis globais da buscab
int buscab(){ // declaro a int buscab
int ini=1, fim=n, meio; // declaro ini, fim e meio
while(ini>=fim){ // enquanto houver alguma posição intervalo a ser olhado
meio=(ini+fim)/2; // meio recebe a posição do meio do intervalo
// se o elemento do meio for o procurado, retorno seu valor
if(vetor[meio-1]>vetor[meio] && vetor[meio+1]>vetor[meio]){
return vetor[meio];
}
// se a sequencia está decrescendo, então o maior está para trás
if(vetor[meio+1]>vetor[meio]){
fim=meio-1;
}
// se a sequência está crescendo, então o maior está para frente
if(vetor[meio+1]<vetor[meio]){
ini=meio+1;
}
}
}Note que, em alguns problemas podemos usar a busca binária em um vetor ordenado com números de 1 a n para chutarmos a sua resposta (n é a resposta máxima) e depois testarmos se ela é válida. Imagine que queremos um inteiro resp mínimo que resolve o problema e todos os outros maiores que ele também resolvem, mas buscamos o menor. Suponha também que testar um número como resposta leva tempo O(n). Se fôssemos testar um por um todos os números, do menor para o maior, a complexidade seria **n*O(n) = O(n²). Mas se usarmos a busca binária para procurarmos a resposta, buscando o primeiro número que funciona, só usaríamos log n** consultas, o que daria uma complexidade de \(O(n \log{n})\).
O código seria bem simples: testo se o número do meio do intervalo funciona. Se ele funcionar, o guardo em alguma variável, e procuro um menor que ele que também funcione, com busca binária, olhando agora para a metade do intervalo que está antes do meio. Se o número não funcionar, então a resposta é maior que ele e devo procurar a na metade do intervalo que vem depois do meio. Segue, para exemplo, a implementação de uma busca binária que encontra, em log n, o primeiro número de um vetor ordenado int vetor[100100], que é maior ou igual a um int x.
int n, vetor[100100];
int buscab(int x){ // declaro a função buscab, que recebe um int como parâmetro
// declaro os inteiros ini, meio, fim e resp
int ini=1, fim=n, meio, menor_resp; // ini já começa com 1 e fim com n
while(ini<=fim){ // enquanto houver algum elemento no intervalo
meio=(ini+fim)/2; // meio recebe a posição do meio
if(vetor[meio]>=x){ // se vetor[meio] for maior ou igual a x
fim=meio-1; // então o primeiro elemento maior ou igual a x pode estar atrás de meio
menor_resp=vetor[meio]; // e guardo o valor de vetor[meio], caso não haja tal elemento atrás de meio
}
// se vetor[meio] ainda é menor que x
if(vetor[meio]<x) ini=meio+1; // então devo olhar na metade do vetor que está depois de meio
}
return menor_resp; // retorno o valor de menor_resp
}public class BuscaSequencialBinaria {
/**
* @param args
* the command line arguments
*/
public static void main(String[] args) {
// TODO código de testes aqui.
int[] vetorBuscaSequencial = { 10, 25, 75, 85, 1, -1, 61, 80 };
int[] vetorBuscaBinariaIterativa = { 1, 2, 30, 41, 73, 81, 90, 101 };
int[] vetorBuscaBinariaRecursiva = { 10, 25, 35, 40, 70, 80, 95, 101 };
System.out.println("Sequencial");
System.out.println(BuscaSequencial(vetorBuscaSequencial, 1));
System.out.println(BuscaSequencial(vetorBuscaSequencial, 82));
System.out.println("Iterativa: ");
System.out.println(BuscaBinariaIterativa(vetorBuscaBinariaIterativa, 81));
System.out.println(BuscaBinariaIterativa(vetorBuscaBinariaIterativa, 103));
System.out.println("Recursiva: ");
System.out.println(
BuscaBinariaRecursiva(vetorBuscaBinariaRecursiva, 35, 0, vetorBuscaBinariaRecursiva.length - 1));
System.out.println(
BuscaBinariaRecursiva(vetorBuscaBinariaRecursiva, 98, 0, vetorBuscaBinariaRecursiva.length - 1));
/*
* - Implementar os 3 algoritmos contidos nos slides e utilizar os
* vetores acima como massa de testes, há um vetor para cada exercício.
* - Fazer duas chamadas para cada método, uma em que encontra a posição
* do elemento e outra em que o elemento buscado não está presenta na
* lista. - Printar a resposta de todas as chamadas aos métodos.
*/
}
public static int BuscaSequencial(int[] vetor, int valorBuscado) {
for (int i = 0; i < vetor.length; i++) {
if (valorBuscado == vetor[i]) {
return i;
}
}
return -1;
}
public static int BuscaBinariaIterativa(int[] vetor, int valorBuscado) {
int inicio = 0;
int fim = vetor.length - 1;
int meio = -1;
while (inicio <= fim) {
meio = (inicio + fim) / 2;
if (valorBuscado == vetor[meio]) {
return meio;
} else if (valorBuscado < vetor[meio]) {
fim = meio - 1;
} else {
inicio = meio + 1;
}
}
return -1;
}
public static int BuscaBinariaRecursiva(int[] vetor, int valorBuscado, int inicio, int fim) {
int i = (inicio + fim) / 2;
if (inicio > fim) {
return -1;
} else if (valorBuscado == vetor[i]) {
return i;
} else if (valorBuscado < vetor[i]) {
fim = i - 1;
return BuscaBinariaRecursiva(vetor, valorBuscado, inicio, fim);
} else {
inicio = i + 1;
return BuscaBinariaRecursiva(vetor, valorBuscado, inicio, fim);
}
}
}
package com.foo.bar;
import java.util.Arrays;
public class BuscaBinariaRecursiva {
public static void main(String[] args) {
int[] array = { 1, 8, 34, 67, 9, 6, 78, 12, 56, 41, 90 };
Arrays.sort(array);
System.out.println(Arrays.toString(array));
System.out.println(busca(array, 6));
System.out.println(busca(array, 78));
System.out.println(busca(array, 90));
}
private static int busca(int[] array, int chave) {
return buscaBinariaRecursiva(array, 0, array.length - 1, chave);
}
private static int buscaBinariaRecursiva(int[] array, int menor, int maior,
int chave) {
int media = (maior + menor) / 2;
int valorMeio = array[media];
if (menor > maior)
return -1;
else if(valorMeio == chave)
return media;
else if (valorMeio < chave)
return buscaBinariaRecursiva(array, media+1, maior, chave);
else
return buscaBinariaRecursiva(array, menor, media-1, chave);
}
}