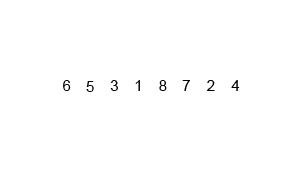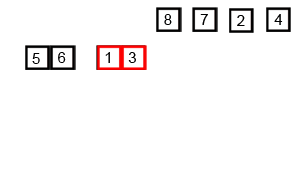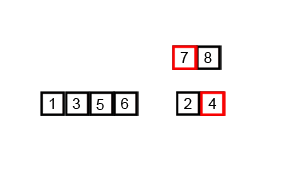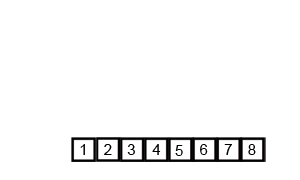MergeSort
Divisão e conquista é um método amplamente conhecido e utilizado na programação competitiva em diversas áreas: grafos, estruturas de dados, análises de sequências, etc. A ideia é que, para resolver um problema, pode ser mais fácil dividi-lo em casos menores, mais fáceis e resolvê-los, um a um, para depois juntá-los, de modo a resolver o caso maior. Como a ideia gira em torno da divisão do problema em subcasos, este método geralmente é implementado com o auxílio de funções recursivas.
Uma das aplicações mais simples e conhecidas de Divisão e Conquista é algoritmo do Merge Sort, um tipo de ordenação com complexidade O(n log n). Suponha que tenhamos que ordenar um vetor. Já conhecemos alguns algoritmos quadráticos que resolvem o problema. Entretanto, o problema fica muito mais fácil se dividimos o vetor em duas metades, as ordenamos, e só então tivéssemos que uni-las de forma a gerar o vetor final ordenado.
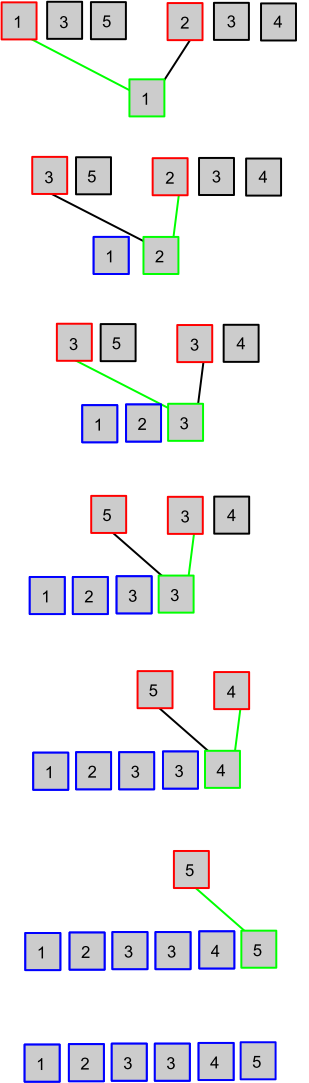
Note que o problema fica muito mais fácil: basta que adicionemos um a um os elementos dos dois vetores, escolhendo sempre o menor. Isso fica fácil pois, como os vetores já estão ordenados, basta escolher o menor entre os primeiros elementos de cada vetor e depois retirá-lo. A seguinte imagem dá uma boa ilustração de com unir dois vetores ordenados em um vetor maior, também ordenado:
A pergunta é: com ordenar magicamente as metades do meu vetor? Basta que o Merge Sort seja uma função recursiva, para que eu chame a própria função em cada metade do vetor que quero ordenar! Se você ainda não entendeu bem o que a função deve fazer, observe esta animação da Wikipédia:
O algoritmo é simples e, para facilitar ainda mais a ordenação, usaremos o vector. No momento, você deve saber muito pouco sobre ponteiros, mas por enquanto basta a seguinte informação: se em uma função, ao invés de receber como parâmetro uma variável x, receber o seu endereço endereço &x, a função irá trabalhar diretamente com a variável original, ou seja, as mudanças que a função fizer na variável irão alterar a variável original que foi passada como parâmetro. Deste modo, se quero implementar a função merge_sort que de fato altera e ordena o vector v, ela não receberá um simples vector como parâmetro, mas o endereço do vector que quero ordenar, ou seja, a declaro da forma void merge_sort(vector &v){}. Vale ressaltar que, uma vez declarada assim, não precisamos mais nos preocupar com o &, pois passamos normalmente os parâmetros sem ele na hora da chamada da função, e ela já entenderá que estou trabalhando com o endereço da variável.
Vamos agora pensar na implementação da função merge_sort, que deve ordenar o vector v. Se v tiver um único elemento, ele já está ordenado, logo a função não precisa fazer nada, e retornamos. Caso contrário, precisamos usar da recursão para implementar a divisão e conquista. O primeiro passo é criar dois vetores auxiliares u1 e u2. No primeiro, colocaremos a primeira metade de v, e no segundo, a segunda. Mais especificamente, se v tem s elementos, u1 ficará com os de índice entre 0 e s/2-1, quanto que u2 ficará com os de índice entre s/2 e s-1. O próximo passo é ordenar u1 e u2, e faço isso chamando o merge_sort para cada um deles, com os comados merge_sort(u1) e merge_sort(u2). Agora, devo uni-los em v. Vamos declarar as variáveis ini1 e ini2, que irão guardar as primeiras posições de u1 e u2, respectivamente, que ainda não foram utilizados, começando, portando, com o valor 0.
Agora, vamos percorrer v, do começo ao fim, colocando em cada posição o menor número de u1 ou u2 que ainda não foi utilizado. Para isso, basta olharmos, para cada posição i de v que iremos preencher, quem é o menor: u1[ini1] ou u2[ini2], pois eles são os menores elementos ainda não utilizados de cada metade. Se for o menor, é simples, basta que o coloquemos na posição i de v (v[i]=u1[ini1];) indicando que o novo menor número não utilizado de u1 é o próximo, ou seja, ini1+1. Logo, basta aumentar o valor de ini1 em uma unidade (ini1++). Agimos de maneira análoga se u2[ini2] for o menor.
Note que a implementação acima pode trazer problemas quando já percorri, por exemplo, todo o vetor u1 e tento acessar sua próxima posição, pois ela não existe e acesso memória inválida. Resolver este problema é simples, basta que eu nunca percorra todo o vetor u1. Para isso, basta adicionar nele, antes de começar a uni-lo com u2 um número muito grande que certamente ficará por último e será maior que os s números colocados em v. O chamarremos de INF, e seu valor depende do tamanho dos números que podem estar em v (ele deve ser maior que qualquer um deles). Faremos o mesmo com u2.
Após percorrer todas as posições de v, ele estará completamente ordenado, e posso terminar a função. Segue seu código para melhor entendimento:
#include <vector> // para o uso de vector
// neste código, irei definir INF como 1 bilhão
#define INF 1000000000
using namespace std;
// função merge_sort que ordena um vector v
void merge_sort(vector<int> &v){
// se o tamanho de v for 1, retorno a função
if(v.size()==1) return;
// se não
// declaro os vetore u1 e u2
vector<int> u1, u2;
// e faço cada um receber uma metade de v
for(int i=0;i<v.size()/2;i++) u1.push_back(v[i]);
for(int i=v.size()/2;i<v.size();i++) u2.push_back(v[i]);
// ordeno u1 e u2
merge_sort(u1);
merge_sort(u2);
// e adiciono INF ao final de cada um deles
u1.push_back(INF);
u2.push_back(INF);
// declaro ini1 e ini2 com valore inicial zero
int ini1=0, ini2=0;
// percorro cada posição de v
for(int i=0;i<v.size();i++){
// se o menor não usado de u1 for menor o mesmo em u2
if(u1[ini1]<u2[ini2]){
// então o coloco em v
v[i]=u1[ini1];
// e incremento o valor de ini1
ini1++;
}
// caso contrário, faço o análogo com u2 e ini2
else{
v[i]=u2[ini2];
ini2++;
}
}
// por fim, retorno a função merge_sort
return;
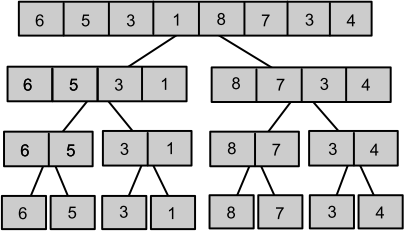
}Agora, façamos uma rápida análise da complexidade deste algoritmo. Para isso, observe antes a seguinte imagem, que representa as chamadas recursivas da função merge_sort em um determinado vetor:
Suponha agora a mesma árvore para um vetor qualquer de \(n\) posições. Observe que, na linha \(i\) da árvore de recursão (começando da linha \(0\)) temos que unir \(2^i\) vetores ordenados de tamanho \(\frac{n}{2^i}\). Como já vimos que juntar dois vetores ordenados tem complexidade \(O(n)\) (onde \(n\) é o tamanho do vetor final, pois usa um único for para preencher todo o vetor), estaremos repetindo, em cada linha, \(2^i\) vezes uma operação de complexidade \(O\left(\frac{n}{2^i}\right)\), o que gera, em cada linha uma complexidade igual a \(O\left(2^i\cdot\frac{n}{2^i}\right)=O(n)\). Mas quantas linhas a função chamará? Repare que dividiremos o vetor ao meio até que só reste \(1\) elemento em cada intervalo, logo, sendo \(m\) a quantidade de linhas, \(\frac{n}{2^m}=1\Leftrightarrow n=2^m\Leftrightarrow\log_2n=\log_2 2^m=m\Leftrightarrow m=\log_2n\). Logo, como são \(\log_2n\) linhas, repetiremos\(\log_2n\) vezes uma operação de complexidade \(O(n)\), o que gera uma complexidade de \(O(n\log n)\) (em informática, ao usarmos o termo \(\log\), nos referimos a logaritmo na base 2, não na base 10).
Agora, tente implementar esta e outras aplicações do método da Divisão e conquista. Lembre-se, novamente, que para usar um ponteiro como um parâmetro em uma função, só precisamos usar o & na hora de declarar a função, e usamos o nome normal da variável (sem o &) tanto no corpo da função como na hora de chamá-la no código.