Programação Dinâmica
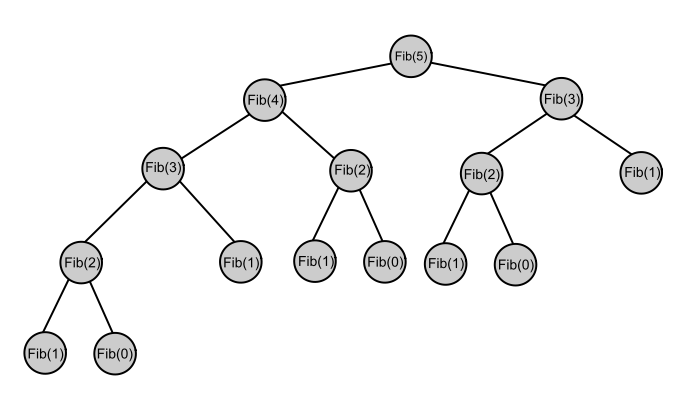
Na aula de funções recursivas, vimos como calcular o n-ésimo número da sequência de Fibonacci. Foi mostrada, também, a árvore de recursão de calcular o 5º número da sequência de Fibonacci, que mostra todas as chamadas que temos que fazer dessa função. Reveja:
Note que o Fib(2), por exemplo, é recalculado 3 vezes na árvore, o que gera o recálculo, para cada chamada do Fib(2) de dois outros valores: Fib(0) e Fib(1). Percebe como sempre chamar a recursão é ineficiente? O número de chamadas em uma função que calcula o Fibonacci cresce exponencialmente e, se formos calcular o Fib de números maiores que 60, já levamos TLE na maioria dos corretores. Imagine uma chamada de Fib que teria que recalcular o valor de Fib(5): ele teria que chamar, novamente, todas os 14 valores de Fib mostrados na árvore acima, mas, e se salvarmos o valor de Fib(5) em algum lugar, depois que o calcularmos? Assim, da próxima vez que precisássemos do valor de Fib(5), teríamos ele guardado sem termo que chamar nenhuma outra função, acessando-o em O(1)! Bastava que guardássemos uma variável com o valor de Fib(5), começando com -1, por exemplo e, quando fôssemos chamar a função, iríamos verificar se o valor lá salvo ainda é -1. Se fosse, então ainda não calculamos esse valor, mas assim que terminássemos, iríamos trocar o valor de da variável de -1 para o valor de 5, fazendo com que, das próximas vezes, bastasse retornar o valor lá salvo. Mas por que fazer isso só com 5?
A ideia de Programação Dinâmica (ou Dynamic Programming (DP), em inglês) é evitar o recálculo de uma função para os mesmos parâmetros que já calculamos alguma vez, salvando todos os resultados que já obtemos até então, calculando o valor da função apenas se ele nunca foi calculado. Assim, só calculamos cada valor da função uma única vez! Chamamos de estado da DP um conjunto de parâmetros que define a situação que ela precisa calcular, e se ela passar pelo mesmo estado duas vezes, ela só precisa calcular seu valor uma vez e guardá-lo para o futuro, se ela precisar. No caso que estamos olhando (Fibonacci), os possíveis estados da DP são as possíveis posições da sequência que ela quer calcular.
Vamos tentar refazer a função que calcula o n-ésimo termo da sequência de Fibonacci de maneira mais eficiente. Para tal, vamos criar um vetor auxiliar int dp[MAXN], onde MAXN é a maior posição da sequência que posso querer calcular. Ele começará com todos os valores iguais a -1 (pois sei que nenhum termo da sequência em posição positiva tem esse valor). Assim, se o valor de dp[i] for -1, então ainda não calculei esse valor. Agora basta refazer a função fib fazendo-a verificar, primeiramente, se já tenho salvo, em dp[x] (“if(dp[x]!=-1)”), o valor de fib(x), retornando-o se isso ocorrer. Caso eu ainda não tenha calculado esse valor, faço a função recursiva e lembro de salvar o valor calculado em dp[x] antes de retornar a função! Uma pequena observação é que existe uma função da cstring chamada memset que faz todos as posições de um array receberem algum valor escolhido. Ela tem três parâmetros e a seguinte gramática (“memset(nome_do_vetor, valor, sizeof(nome_do_vetor));”). Ela troca todos os bytes do vetor pelo valor escolhido e, como um int tem 4 bytes, não podemos usá-la em todos os casos. Saiba que ela funciona para 0 e -1, o que felizmente é o nosso caso. Segue o código para melhor entendimento:
#include <iostream>
#include <cstring> // biblioteca do memset
#define MAXN 1000100
int n, dp[MAXN]; // declaro n e o vetor auxiliar
int fib(int x){ // declaro a função int fib(int x)
// se já calculei, alguma vez, o valor de fib(x)
if(dp[x]!=-1) return dp[x]; // retorno o que está salvo em dp[x]
// se não, calculo a função normalmente
if(x==0) return 0; // se x=0, retorn 0
if(x==1) return 1; // se x=1, retorn 1
// se não era nenhum dos casos base
dp[x]=fib(x-1)+fib(x-2); // calculo o valor de fib(x) e salvo em dp[x]
return dp[x]; // para só então retornar o valor que deixei salvo lá
}
int main(){
memset(dp, -1, sizeof(dp)); // faço todos as posições de dp receberem o valor -1
cin >> n; // leio o valor de n
cout << fib(n) << "\n"; // e imprimo o valor de fib(n)
return 0;
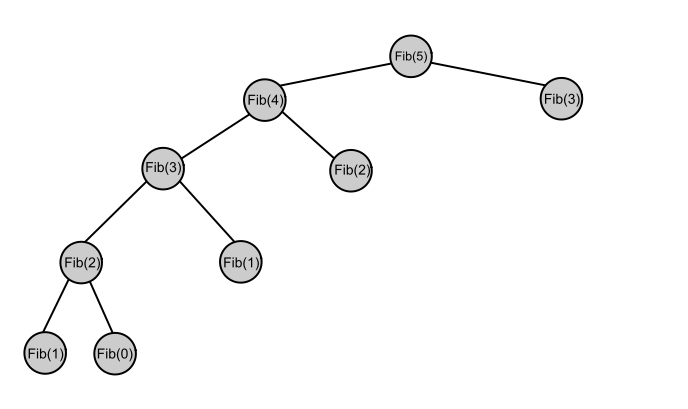
}Observe que, com essa função, evito vária chamadas recursivas, o que otimiza muito a complexidade, pois agora só calculo cada valor da sequência uma única vez. Logo, a complexidade fica O(n), onde n é a posição da sequência que queremos calcular. Para você entender isso melhor, veja como fica a nova árvore de recursão dessa versão mais eficiente da função Fib, que só calcula os valores 1 vez e para a recursão sempre que houver recálculo:
Em qualquer função recursiva, podemos (e devemos) guardar o valores já calculados e evitar recálculo com programação dinâmica. A função fib tem um único parâmetro, por isso podia guardar seu valores em um vetor. Se precisássemos usar uma função de nome dp que recebe dois inteiros como parâmetros, do tipo “int dp(int parametro1, int parametro2){}” iríamos guardar seus valores em uma matriz nxm (“int tab[n+10][m+10];”), onde n** é o maior valor possível de parametro1 e m o maior valor possível de parametro2. Desse modo, iríamos guardar o valor de dp(x, y) em tab[x][y]. Façamos agora algumas observações: As duas últimas linhas da função apresentada:”dp[x]=fib(x-1)+fib(x-2);**” e “return dp[x];” podem ser substituídas por um único comando: “return dp[x]=fib(x-1)+fib(x-2);”, que executa exatamente os dois comando anteriores nessa mesma ordem. Usaremos sempre isso em programação dinâmica.
Tipos de Abordagem
Note que usamos uma função recursiva que chama os casos mais de cima (mais distantes dos casos base) da DP (como chamamos a função que usa programação dinâmica), até chegar aos casos base e só então ir voltando a recursão. Esse tipo de abordagem, em que usamos uma função recursiva para calcular os valores da DP é chamado de abordagem Top-Down, pois começa dos casos de cima e vai descendo até chegar à raiz da DP. Existe outro método, em que fazemos o contrário: construimos os casos base e a partir deles vamos criando os casos mais de cima, até que cheguemos no caso procurado. Esse tipo de abordagem é conhecido como Bottom-Up.
No problema de Fibonacci, isso seria semelhante a criar um vetor de n posições de nome int fib, por exemplo, inicializá-lo com os casos base já feitos (“fib[0]=0; fib[1]=1;”) e então usarmos um for** para percorrê-lo até n, fazendo com que cada posição i receba a soma dos valores guardador nas duas posições anteriores (”fib[i]=fib[i-1]+fib[i-2];“). Ao final do for,bastaria imprimir o valor salvo em fib[n]. Como vamos apenas percorrer o vetor uma vez, a complexidade continua O(n)**. Segue o código para melhor entendimento:
#include <iostream>
#define MAXN 1000100
int fib[MAXN], n; // declaro n e o vetor que usarei na dp
int main(){
cin >> n; // leio o valor de n
fib[0]=0; // defino os casos base da dp
fib[1]=1;
// faço a dp na abordagem Bottom-Up
for(int i=2; i<=n; i++){
fib[i]=fib[i-1]+fib[i-2];
}
cout << fib[n] << "\n" // e imprimo o valor salvo em fib[n]
return 0;
}A complexidade de uma DP depende da sua quantidade de estados e da complexidade do cálculo de cada estado (desconsiderando a recursão), sendo o produto destes, pois cada estado é calculado uma única vez. No caso do Fibonacci, observe que o processamento da função (recursiva ou não) é constante. Deste modo, sua complexidade é simplesmente o número de estados, que no caso do Fibonacci é n, logo sua complexidade é linear (O(n)).